จากข้อมูลแผ่นดินไหวที่บันทึกเก็บไว้ตั้งแต่อดีตจนปัจจุบัน นักแผ่นดินไหวหลายคนเคยเอามานั่งดู และพบว่าจำนวนการเกิดแผ่นดินไหวโดยภาพรวมในแต่ละช่วงเวลาและในพื้นที่ใดๆ “แผ่นดินไหวเล็กจะมีอัตราการเกิดบ่อยกว่าแผ่นดินไหวใหญ่” เช่น แผ่นดินไหวขนาด 2.0 เกิดขึ้นทั่วโลกประมาณ 1,000,000 เหตุกาณ์/ปี ในขณะที่แผ่นดินไหวขนาด 5.0 เกิดโดยเฉลี่ย 2,000 เหตุการณ์/ปี ซึ่งต่อมา Ishimoto และ Iida (1939) และ Gutenberg และ Richter (1944) ได้คนพบความสัมพันธ์ระหว่างระหว่างจำนวนการเกิดของแผ่นดินไหวในแต่ละขนาด และนำเสนอสมการความสัมพันธ์ การกระจายตัวความถี่-ขนาดแผ่นดินไหว (Frequency-Magnitude Distribution, FMD) หรือที่นักแผ่นดินไหวบางกลุ่มวิจัย เรียกว่า สมการกูเต็นเบิร์ก-ริกเตอร์ (Gutenberg-Richter Relationship) ดังแสดงในสมการ (1) (ดูรูปประกอบ)

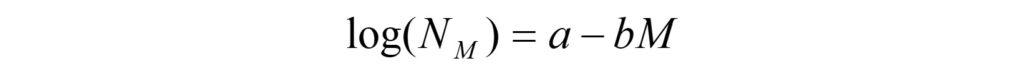
กำหนดให้ N_M คือ จำนวนหรืออัตราการเกิดแผ่นดินไหวสะสม (cumulative number) ของแผ่นดินไหวที่มีขนาด ≥ M ส่วนค่า a และค่า b คือ ค่าคงที่มีค่าบวก ซึ่งจะมีค่าแตกต่างกันไปในแต่ละช่วงเวลาและพื้นที่ใดๆ และเป็นตัวแปรสำคัญที่สื่อถึง พฤติกรรมการเกิดแผ่นดินไหว (earthquake activity)

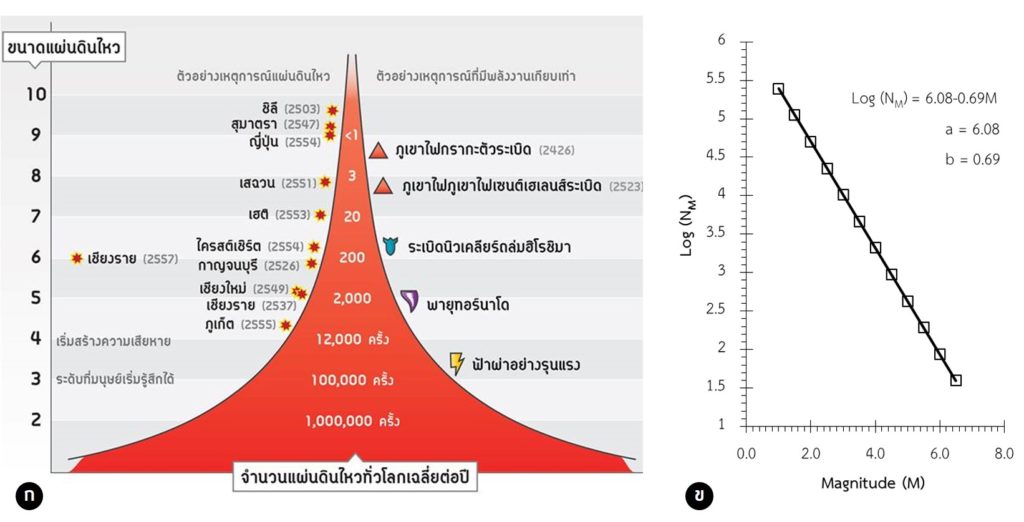
ตัวอย่างเช่น พื้นที่ภูมิภาคอาเซียน Pailoplee และ Choowong (2013) ได้นำข้อมูลแผ่นดินไหวทั้งหมดในพื้นที่ที่ตรวจวัดได้จากเครื่องมือตรวจวัด มาวิเคราะห์จำนวนแผ่นดินไหวในแต่ละขนาด และสร้างกราฟแสดงความสัมพันธ์ FMD และวิเคราะห์ค่า a และค่า b ของแหล่งกำเนิดแผ่นดินไหวสำคัญๆ ในภูมิภาคอาเซียน ผลการวิเคราะห์และสร้างกราฟ FMD แสดงให้เห็นว่าข้อมูลแผ่นดินไหวจากแหล่งกำเนิดแผ่นดินไหวต่างๆ สอดคล้องกับสมการความสัมพันธ์ FMD และสามารถวิเคราะห์ค่า a และค่า b จากส่วนที่เป็นเส้นตรงของสมการความสัมพันธ์ FMD ได้

ซึ่งในทางวิทยาคลื่นไหวสะเทือน (seismology) ค่า a (จุดตัดแกน Y ของสมการความสัมพันธ์ FMD ที่เป็นสมการเส้นตรง) คือ จำนวนหรืออัตราการเกิดแผ่นดินไหวโดยรวมจากทุกขนาดแผ่นดินไหว (log ของจำนวนแผ่นดินไหวสะสมที่มีขนาด ≥ 0) โดยค่า a สูง/ต่ำ หมายถึง จำนวนหรืออัตราการเกิดแผ่นดินไหวโดยรวมสูง/ต่ำ ดังนั้นจากผลการวิเคราะห์บ่งชี้ว่าแหล่งกำเนิดแผ่นดินไหวในพื้นที่ชายแดนภาคเหนือของประเทศไทย-ลาว-พม่า (a = 4.3) มีอัตราการเกิดแผ่นดินไหวโดยรวมสูงกว่าเขตมุดตัวของเปลือกโลกสุมาตรา-อันดามันและรอยเลื่อนสะกาย ตอนกลางของประเทศพม่า (a = 4.1)

ส่วนในกรณีของค่า b (ความชันของสมการความสัมพันธ์ FMD) หมายถึง สัดส่วนของแผ่นดินไหวขนาดใหญ่กว่าต่อแผ่นดินไหวขนาดเล็กกว่า ดังนั้นในพื้นที่ใดๆ ที่มีค่า b ต่ำ บ่งชี้ในเบื้องต้นว่ามีโอกาสเกิดแผ่นดินไหวขนาดใหญ่สูงกว่าบริเวณที่มีค่า b สูง ดังนั้นจากผลการวิเคราะห์ก็บ่งชี้ว่าเขตมุดตัวของเปลือกโลกสุมาตรา-อันดามัน (b = 0.63) และรอยเลื่อนสะกายมีโอกาสเกิดแผ่นดินไหวขนาดใหญ่สูงกว่ารอยเลื่อนสะกาย (b = 0.72) และพื้นที่ชายแดนภาคเหนือของประเทศไทย-ลาว-พม่า (b = 0.80)

อย่างไรก็ตามถึงแม้ว่าแหล่งกำเนิดแผ่นดินไหวใดๆ จะมีพฤติกรรมการเกิดแผ่นดินไหวคล้ายกัน (Pailoplee และ Choowong, 2013) แต่เนื่องจากแหล่งกำเนิดแผ่นดินไหวมีพื้นที่กว้างและอาจได้รับความเค้นทางธรณีแปรสัณฐานที่แตกต่างกันในแต่ละพื้นที่ย่อยภายในแหล่งกำเนิดแผ่นดินไหว ทำให้ในแต่ละแหล่งกำเนิดแผ่นดินไหวอาจมีพฤติกรรมการเกิดแผ่นดินไหวที่แตกต่างกันในรายละเอียด เช่น ตอนเหนือ ตอนกลางหรือตอนใต้ของเขตมุดตัวของเปลือกโลกสุมาตรา-อันดามัน อาจมีพฤติกรรมการเกิดแผ่นดินไหวโดยรวมคล้ายกัน แต่แตกต่างกันในรายละเอียด

ดังนั้นนอกจากการประเมินพฤติกรรมการเกิดแผ่นดินไหวโดยรวมจากสมการความสัมพันธ์ FMD นักแผ่นดินไหวยังสามารถประเมินการกระจายตัวเชิงพื้นที่ของพฤติกรรมการเกิดแผ่นดินไหวได้ จากการแบ่งแหล่งกำเนิดแผ่นดินไหวใดๆ ออกเป็นพื้นที่ย่อยขนาดเท่ากัน และนำข้อมูลแผ่นดินไหวที่เคยเกิดขึ้นในแต่ละพื้นที่ย่อยมาสร้างกราฟแสดงความสัมพันธ์ FMD และวิเคราะห์ค่า a และค่า b ตามลำดับ หลังจากนั้นสร้างแผนที่แสดงการกระจายตัวเชิงพื้นที่ของตัวแปรดังกล่าว เช่น แผนที่แสดงการกระจายตัวเชิงพื้นที่ของค่า a และค่า b รวมทั้งค่าสถิติอื่นๆ ที่แสดงถึงความแม่นยำของการวิเคราะห์สมการความสัมพันธ์ FMD เช่น ส่วนเบี่ยงเบนมาตรฐานของค่า b (standard deviation, SD) และเปอร์เซนต์ความสอดคล้องระหว่างข้อมูลแผ่นดินไหวที่ใช้ในการวิเคราะห์และความสัมพันธ์ทางคณิตศาสตร์ของสมการความสัมพันธ์ FMD (% of goodness fit of FMD) (Pailoplee และ Boonchaluay, 2016)

สำหรับการวิเคราะห์สมการความสัมพันธ์ FMD ในบริเวณหมู่เกาะฟิลิปปินส์และพื้นที่ข้างเคียง Pailoplee และ Boonchaluay (2016) แบ่งพื้นที่ศึกษาออกเป็นพื้นที่ย่อยขนาด 110×110 ตารางกิโลเมตร (ประมาณ 1^ox1^o) และใช้ข้อมูลแผ่นดินไหวที่เกิดขึ้นในแต่ละพื้นที่ย่อยมาสร้างกราฟแสดงความสัมพันธ์ FMD และวิเคราะห์ค่า a และค่า b รวมทั้งค่าสถิติอื่นๆ แต่เนื่องจากบางพื้นที่ เช่น พื้นที่โดยรอบร่องลึกก้นสมุทรปาลาวัน [8] ร่องลึกก้นสมุทรซูลูอาชิเพลาโก [12] และตอนใต้ของร่องลึกก้นสมุทรซูลู [13] มีข้อมูลแผ่นดินไหวไม่เพียงพอต่อการวิเคราะห์สมการความสัมพันธ์ FMD อย่างมีนัยสำคัญ Pailoplee และ Boonchaluay (2016) จึงไม่นำเสนอผลการวิเคราะห์ค่า a และค่า b รวมทั้งค่าสถิติอื่นๆ ในพื้นที่ดังกล่าว

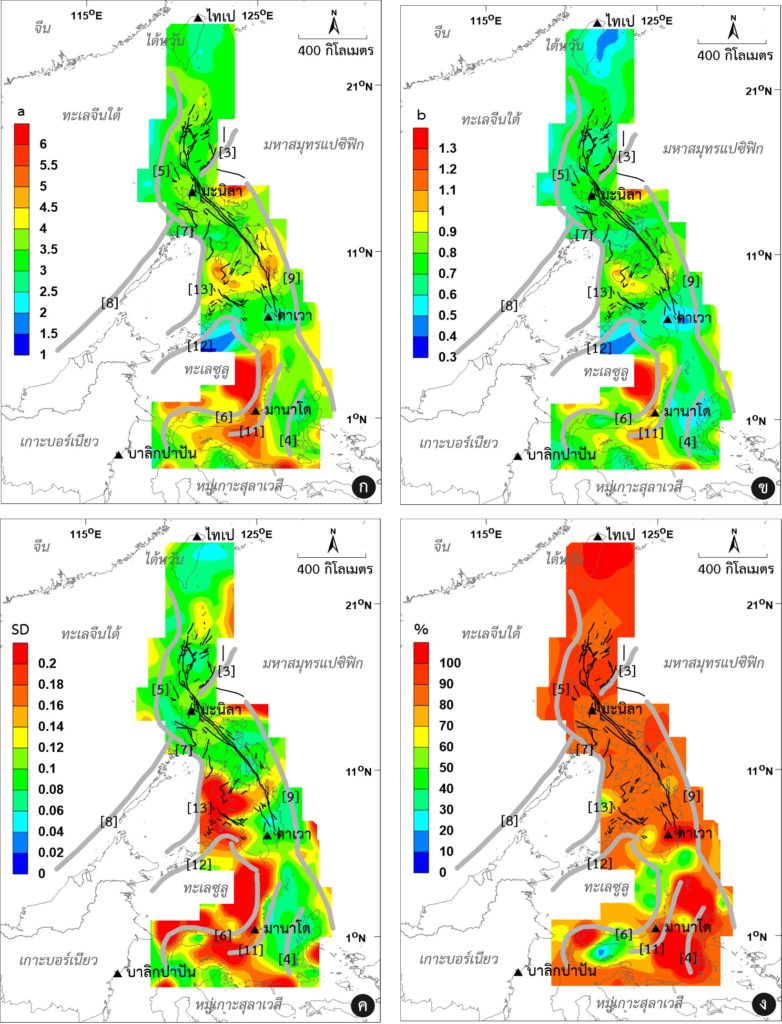
จากแผนที่แสดงการกระจายตัวของค่า a แสดงพื้นที่ที่มีค่า a สูงกว่าพื้นที่ข้างเคียงอย่างชัดเจน (a = 4.0-5.0) จำนวน 3 พื้นที่ ได้แก่ 1) ทางตะวันออกของเมืองมะนิลา (Manila) 2) ตอนเหนือของเมืองดาเวา (Davao) ซึ่งมีรอยเลื่อนกระจายตัวอยู่อย่างหนาแน่น และ 3) พื้นที่โดยรอบเมืองมานาโด (Manado) ซึ่งอยู่ใกล้กับร่องลึกก้นสมุทรมินาฮาสสาและเขตมุดตัวของเปลือกโลกซันกิลดับเบิ้ล ในขณะที่ทางตอนเหนือของ ร่องลึกก้นสมุทรซูลูอาชิเพลาโกแสดงค่า a ต่ำ ในช่วง 1.0-2.0 และหากพิจารณาค่า b ก็พบว่าการกระจายตัวเชิงพื้นที่ของค่า b ส่วนใหญ่สอดคล้องกับการกระจายตัวเชิงพื้นที่ของค่า a โดยพื้นที่ซึ่งมีค่า a สูง/ต่ำ จะมีค่า b สูง/ต่ำ อย่างสัมพันธ์กัน

ในส่วนของความแม่นยำของการวิเคราะห์สมการความสัมพันธ์ FMD ในพื้นที่ศึกษา พบว่าส่วนเบี่ยงเบนมาตรฐานของค่า b มีค่า < 0.2 บ่งชี้ว่าทั้งค่า a และค่า b ที่วิเคราะห์ได้มีความแปรผันต่ำ นอกจากนี้เปอร์เซนต์ความสอดคล้องระหว่างข้อมูลแผ่นดินไหวที่ใช้ในการวิเคราะห์และความสัมพันธ์ทางคณิตศาสตร์ของสมการความสัมพันธ์ FMD พบว่าพื้นที่ส่วนใหญ่มีค่า > 80% บ่งชี้ว่าผลการวิเคราะห์ที่ได้มีความน่าเชื่อเถือในทางสถิติ

ในกรณีของการวิเคราะห์สมการความสัมพันธ์ FMD ของกลุ่มรอยเลื่อนตามแนวราบที่วางตัวอยู่บริเวณชายแดนภาคตะวันตกของประเทศไทย-พม่า เช่น กลุ่มรอยเลื่อนเจดีย์สามองค์ กลุ่มรอยเลื่อนศรีสวัสดิ์ กลุ่มรอยเลื่อนพานหลวง ฯลฯ Pailoplee (2014a) ตรวจพบค่า a สูงกว่าพื้นที่ข้างเคียง (a = 3.2-4.1) ทางตอนเหนือของกลุ่มรอยเลื่อนตามแนวราบดังกล่าว ซึ่งอยู่ใกล้กับรอยเลื่อนสะกาย ตอนกลางของประเทศพม่า ในขณะที่กลุ่มรอยเลื่อนตามแนวราบทางตอนใต้ ในพื้นที่ภาคตะวันตกของประเทศไทยส่วนใหญ่มีค่า a ต่ำ เมื่อเปรียบเทียบกับพื้นที่ข้างเคียง (a = 1.4-2.6) ดังที่อธิบายในข้างต้น ค่า a สูง/ต่ำ หมายถึง จำนวนหรืออัตราการเกิดแผ่นดินไหวโดยรวมสูง/ต่ำ ดังนั้นจากก บ่งชี้ในเบื้องต้นว่าพื้นที่ทางตอนเหนือมีอัตราการเกิดแผ่นดินไหวโดยรวมสูงกว่าพื้นที่ทางตอนใต้ของกลุ่มรอยเลื่อนตามแนวราบที่วางตัวอยู่บริเวณชายแดนภาคตะวันตกของประเทศไทย-พม่า

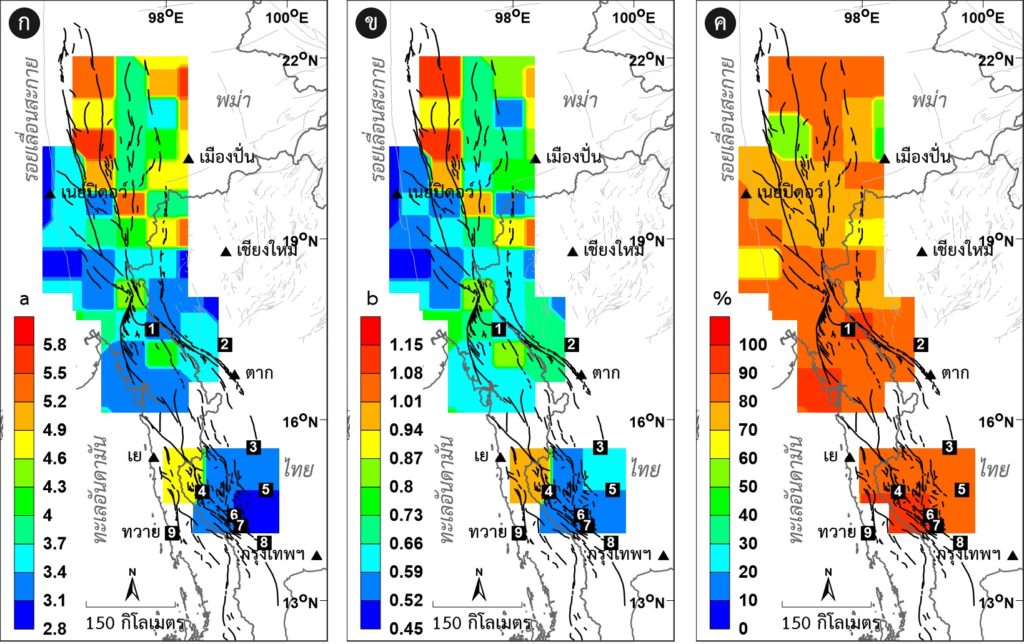
หากพิจารณาค่า b พบว่าการกระจายตัวเชิงพื้นที่ของค่า b ส่วนใหญ่สอดคล้องกับการกระจายตัวเชิงพื้นที่ของค่า a เช่นเดียวกับการวิเคราะห์สมการความสัมพันธ์ FMD ในพื้นที่หมู่เกาะฟิลิปปินส์ (Pailoplee และ Boonchaluay, 2016) โดยพื้นที่ซึ่งมีค่า a สูง/ต่ำ จะมีค่า b สูง/ต่ำ อย่างสัมพันธ์กัน นอกจากนี้ เปอร์เซนต์ความสอดคล้องระหว่างข้อมูลแผ่นดินไหวที่ใช้ในการวิเคราะห์และความสัมพันธ์ทางคณิตศาสตร์ของสมการความสัมพันธ์ FMD มีค่าอยู่ในช่วง 80-100% บ่งชี้ว่าผลการวิเคราะห์ค่า a และค่า b ที่ได้มีความแม่นยำและมีนัยสำคัญในทางสถิติ (Pailoplee, 2014a)

จากตัวอย่างผลการวิเคราะห์และสร้างแผนที่แสดงค่าต่างๆ ของสมการความสัมพันธ์ FMD ในเบื้องต้น พบว่าในแต่ละพื้นที่ย่อยของแหล่งกำเนิดแผ่นดินไหวมีพฤติกรรมการเกิดแผ่นดินไหวเฉพาะตัว ซึ่งทั้งค่า a และค่า b ที่ได้ในแต่ละพื้นที่ย่อย นักแผ่นดินไหวสามารถนำค่าดังกล่าวมาวิเคราะห์ต่อถึง พฤติกรรมการเกิดแผ่นดินไหว (earthquake activity) ในรูปแบบต่างๆ ได้ โดยแสดงอยู่ในรูปแบบของ 1) แผ่นดินไหวขนาดใหญ่ที่สุด 2) คาบอบุติซ้ำการเกิดแผ่นดินไหว และ 3) โอกาสเกิดแผ่นดินไหว

1) แผ่นดินไหวขนาดใหญ่ที่สุด (Maximum Magnitude)

จากสมการความสัมพันธ์ FMD ซึ่งนำเสนอโดย Ishimoto และ Iida (1939) และ Gutenberg และ Richter (1944) ในเวลาต่อมา Yadav และคณะ (2011) ได้ประยุกต์ใช้สมการความสัมพันธ์ FMD ดังกล่าวเพื่อประเมินพฤติกรรมการเกิดแผ่นดินไหวในรูปแบบต่างๆ โดยปรับเทียบสมการความสัมพันธ์ FMD ให้อยู่ในรูปแบบของสมการ (2)

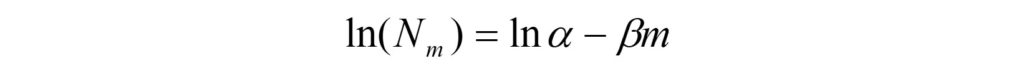
กำหนดให้ alpha และ beta คือ ค่าคงที่ซึ่งสัมพันธ์กับค่า a และค่า b ในรูปแบบของ alpha = exp(a.ln(10)) และ beta = b.ln(10) โดยจากตัวแปรดังกล่าว Yadav และคณะ (2011) นำเสนอวิธีการประเมินแผ่นดินไหวขนาดใหญ่ที่สุด u_t ที่สามารถเกิดขึ้นได้ในช่วงเวลา t (หน่วย ปี) ที่พิจารณา นับตั้งแต่เวลาล่าสุดของฐานข้อมูลแผ่นดินไหวที่ใช้ในการวิเคราะห์ ดังแสดงในสมการ (3)

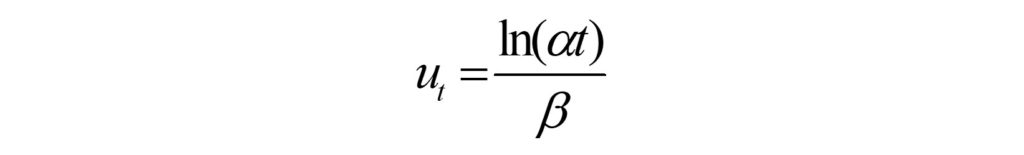
2) คาบอบุติซ้ำการเกิดแผ่นดินไหว (Return Period)

นอกจากนี้ Yadav และคณะ (2011) ได้ประเมินคาบอุบัติซ้ำการเกิดแผ่นดินไหวในแต่ละขนาดจากสมการ (4)

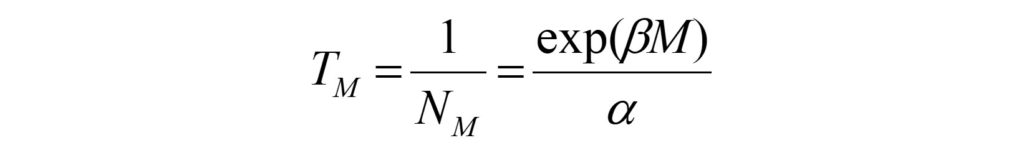
กำหนดให้ T_M คือ คาบอุบัติซ้ำการเกิดแผ่นดินไหวในแต่ละขนาด M (หน่วย ปี) ซึ่งเป็นส่วนกลับของจำนวนหรือความถี่ของการเกิดแผ่นดินไหว N_M

3) โอกาสเกิดแผ่นดินไหว (Probability of Occurrence)

นอกจากแผ่นดินไหวขนาดใหญ่ที่สุดที่สามารถเกิดขึ้นได้และคาบอุบัติซ้ำการเกิดแผ่นดินไหว Yadav และคณะ (2011) ยังประเมินและแสดงพฤติกรรมการเกิดแผ่นดินไหวของแหล่งกำเนิดแผ่นดินไหวในรูปแบบของโอกาสเกิดแผ่นดินไหว (probability of occurrence) (หน่วย %) ในแต่ละขนาดแผ่นดินไหวและช่วงเวลาที่พิจารณา ดังแสดงในสมการ (5)

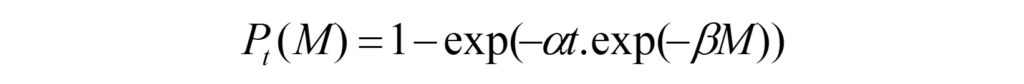
กำหนดให้ P_t(M) คือ โอกาสเกิดแผ่นดินไหวขนาด M ในช่วงเวลาอีก t ปี ซึ่งโดยทั่วไปสามารถแสดงในรูปแบบของกราฟแสดงความสัมพันธ์ระหว่างโอกาสเกิดแผ่นดินไหวและขนาดแผ่นดินไหว เช่น แสดงผลการประเมินโอกาสเกิดแผ่นดินไหวขนาดต่างๆ (4.0-7.0 M_w) ในช่วงเวลาที่พิจารณา (10-100 ปี) ประเมินจาก 6 จังหวัด ทางภาคเหนือของประเทศไทย (Pailoplee และ Charusiri, 2015a) และเขื่อนขนาดใหญ่ 3 เขื่อน ในภาคตะวันตกของประเทศไทย (Pailoplee, 2014a)

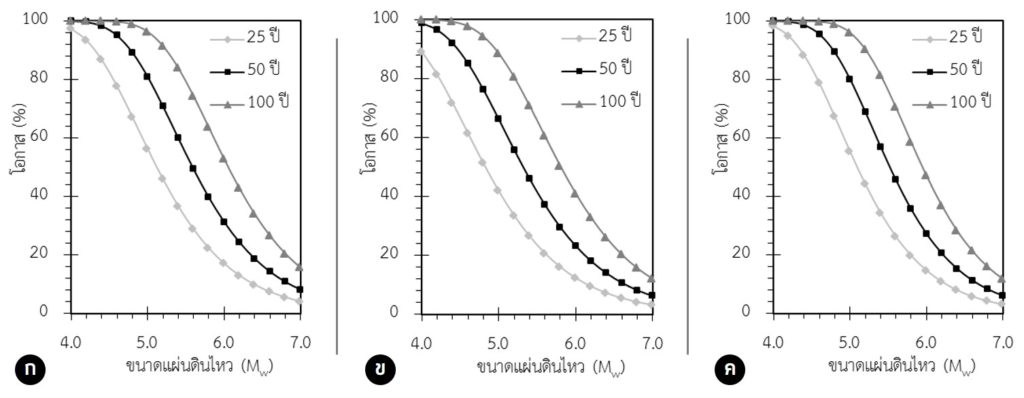
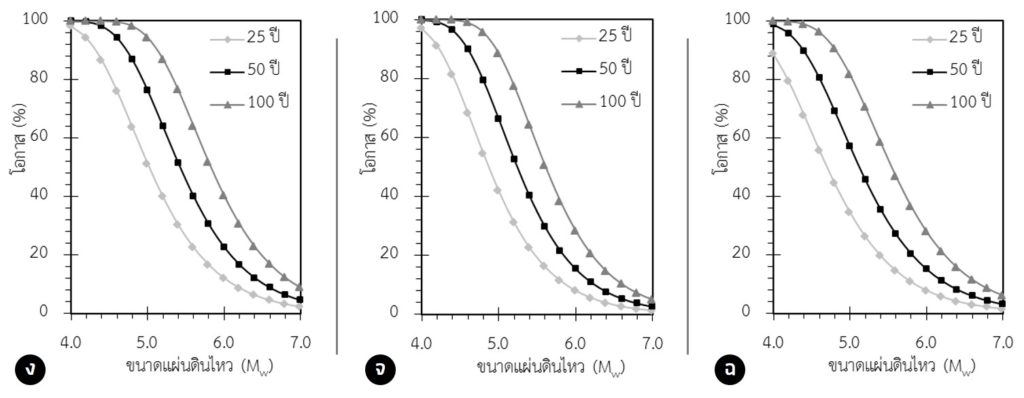
ซึ่งจากรูป ก-ค บ่งชี้ว่าจังหวัดเชียงใหม่ ลำพูน และจังหวัดลำปาง มีโอกาสประมาณ 50% 70% และ 90% ที่จะเกิดแผ่นดินไหวขนาด 5.0 M_w ในอีก 25 ปี 50 ปี และ 100 ปี ตามลำดับ ในขณะที่แผ่นดินไหวขนาด 6.0 M_w มีโอกาสประมาณ 15-40% ที่จะเกิดขึ้นในอีก 25-100 ปี นอกจากนี้ในพื้นที่จังหวัดแพร่ พะเยาและจังหวัดอุตรดิตถ์ (รูป ง-ฉ) มีโอกาสเกิดแผ่นดินไหวขนาด 6.0 M_w ประมาณ 30% ในอีก 100 ปี ในขณะที่จังหวัดเชียงใหม่ ลำพูน และจังหวัดลำปาง ซึ่งตั้งอยู่ใกล้กับรอยเลื่อนแม่ทาและรอยเลื่อนลำปาง-เถิน มีพฤติกรรมการเกิดแผ่นดินไหวสูงกว่าจังหวัดแพร่ พะเยาและจังหวัดอุตรดิตถ์

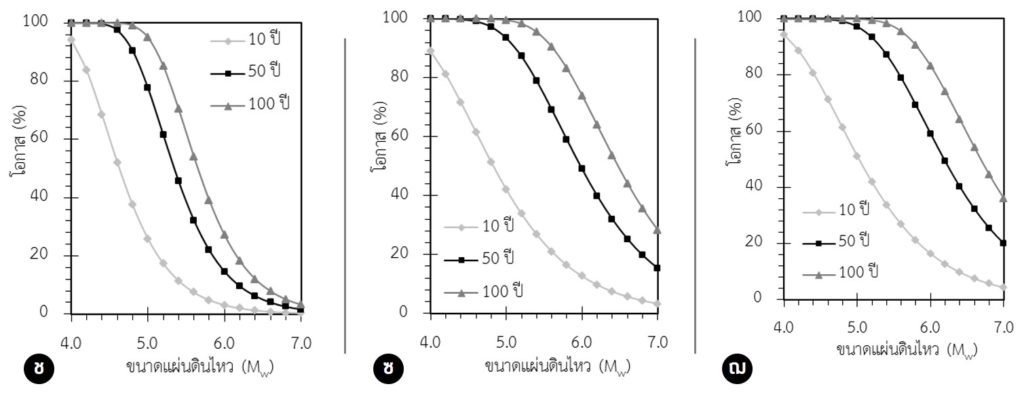
ในกรณีของเขื่อนขนาดใหญ่ในภาคตะวันตกของประเทศไทย Pailoplee (2014a) รายงานว่าเขื่อนศรีนครินทร์และเขื่อนท่าทุ่งนา (รูป ช-ซ) ซึ่งตั้งอยู่ใกล้กับกลุ่มรอยเลื่อนตามแนวราบบริเวณชายแดนภาคตะวันตกของประเทศไทย-พม่า มีโอกาส 96-97% 59-62% และ 20-25% ที่แผ่นดินไหวขนาด 5.0 M_w 6.0 M_w และ 7.0 M_w จะเกิดขึ้นในอีก 50 ปี หรือหากพิจารณาช่วงเวลาในอีก 100 ปี พบว่าทั้ง 3 เขื่อนดังกล่าว มีโอกาสประมาณ 40% ที่จะเกิดแผ่นดินไหวขนาด 7.0 M_w ในขณะที่เขื่อนวชิราลงกรณ ซึ่งตั้งอยู่ในพื้นที่ซึ่งยังไม่เกิดแผ่นดินไหวในช่วงเวลา 50 ปี ที่ผ่านมา มีโอกาสเพียง 2% และ 10% ที่จะเกิดแผ่นดินไหวขนาด 7.0 M_w ในอีก 50 ปี และ 100 ปี ตามลำดับ (รูป ฌ) (Pailoplee, 2014a)

. . .
บทความล่าสุด : www.mitrearth.org
เยี่ยมชม facebook : มิตรเอิร์ธ – mitrearth